How it Started
It all began with the game of pig. It was the start to the ¨Probability project". It really helped me understand the basics of probability while still being very interesting and fun. Basically you both start with zero points and take turns to throw the dice as many times as you like adding the total at each throw to your score. Throwing one 6 ends the turn and nothing is added to the score for that turn. Throwing a double 6 ends the turn and the total score goes back to zero. This was a game of chance because each throw was its own. The winner is the first player to get 100 or more points
• Probability / Probability is the measure of the likelihood that an event will occur.
• Observed Probability / In probability and statistics, a realization, observation, or observed value, of a random variable is the value that is actually observed (what actually happened).
• Theoretical Probability / The likeliness of an event happening based on all the possible outcomes
• Conditional Probability / Conditional probability is a measure of the probability of an event given that (by assumption, presumption, assertion or evidence) another event has occurred.
• Probability of Multiple Events / Using a multiplication rule formula where you multiply the probability of the first by the second to get the probability of all the events.
• Expected Value / The Predicted Value of a Variable
• Two-Way Tables / A table the lets you organize data which is put into two rows one Vertical and one Horizontal.
• Tree Diagram are a type of diagram that allow you to see all the possible outcomes through branches.
• Joint Probability / A joint probability is a statistical measure where the likelihood of two events occurring together and at the same point in time are calculated.
• Marginal Probability / In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. It gives the probabilities of various values of the variables in the subset without reference to the values of the other variables.
The game I decided to showcase was Basetta. There was many games played but I found the most information about this one which helped me get a good idead on how to play it. We do not know who invented it but we do know it originated in Italy. The game was played by higher class people due to the fact that you could win and lose very big. This game was usually played at gaming dens where people would come together. Although there is no direct game like this today. Although there could be a game that took aspects from Basetta. Chance and probability come into play when the dealer is pulling cards from his deck and the player wants him to pull his card. This is where the chance came into play for our game.
• Probability / Probability is the measure of the likelihood that an event will occur.
• Observed Probability / In probability and statistics, a realization, observation, or observed value, of a random variable is the value that is actually observed (what actually happened).
• Theoretical Probability / The likeliness of an event happening based on all the possible outcomes
• Conditional Probability / Conditional probability is a measure of the probability of an event given that (by assumption, presumption, assertion or evidence) another event has occurred.
• Probability of Multiple Events / Using a multiplication rule formula where you multiply the probability of the first by the second to get the probability of all the events.
• Expected Value / The Predicted Value of a Variable
• Two-Way Tables / A table the lets you organize data which is put into two rows one Vertical and one Horizontal.
• Tree Diagram are a type of diagram that allow you to see all the possible outcomes through branches.
• Joint Probability / A joint probability is a statistical measure where the likelihood of two events occurring together and at the same point in time are calculated.
• Marginal Probability / In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. It gives the probabilities of various values of the variables in the subset without reference to the values of the other variables.
The game I decided to showcase was Basetta. There was many games played but I found the most information about this one which helped me get a good idead on how to play it. We do not know who invented it but we do know it originated in Italy. The game was played by higher class people due to the fact that you could win and lose very big. This game was usually played at gaming dens where people would come together. Although there is no direct game like this today. Although there could be a game that took aspects from Basetta. Chance and probability come into play when the dealer is pulling cards from his deck and the player wants him to pull his card. This is where the chance came into play for our game.
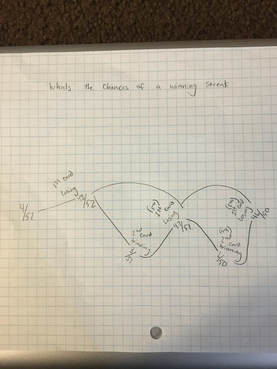
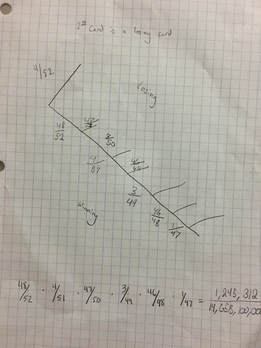
The Question we addressed for our Probability was the possibility of getting a winning streak. The two pictures here show our Tree diagram on the right. On the left it shows more of our calculations to show the probability. Our good understanding of how the game worked really helped on finding out the probabilities of getting a winning streak for our game. This probability decreased or increased depending on how many times the target card had been drawn.
Some Habits Of A Mathematician that I found that helped me a lot throughout this project was starting small and being systematic. A lot of these problems were sometimes hard for me to understand. Starting small and taking my time throughout these problems really helped me to be able to understand them a lot more. Being systematic was also helpful. Taking certain aspects of the problems that I found challenging and then writing specific notes on these parts really helped me understand how to encounter them the next time I saw them.
For me this project overall was interesting, fun, and challenging all at the same time. We first started out with smaller activities but as we progressed everything got a little bit harder. Sometimes it would take me a while to understand a complex problem. Something I found that worked really well for me just stepping back reading the problem a couple of times so I really understood what it was asking. Then taking each part of the problem one step at a time. Since probability was relatively new to me it took me to understand the whole concept. Probability of multiple events was something that really confused me at first since something that was so small created a big probability. After a couple times going over different problems I started to understand the idea. The best part of this project for me was being able to play our game at exhibition. My mom and my partners grandparents really enjoyed our game. Since we really got a good understanding of our game we were able to play our game with no major confusions or problems. Overall I felt like this was a good structured project that I enjoyed.
For me this project overall was interesting, fun, and challenging all at the same time. We first started out with smaller activities but as we progressed everything got a little bit harder. Sometimes it would take me a while to understand a complex problem. Something I found that worked really well for me just stepping back reading the problem a couple of times so I really understood what it was asking. Then taking each part of the problem one step at a time. Since probability was relatively new to me it took me to understand the whole concept. Probability of multiple events was something that really confused me at first since something that was so small created a big probability. After a couple times going over different problems I started to understand the idea. The best part of this project for me was being able to play our game at exhibition. My mom and my partners grandparents really enjoyed our game. Since we really got a good understanding of our game we were able to play our game with no major confusions or problems. Overall I felt like this was a good structured project that I enjoyed.
DP Update #2
My group and I chose to measure a snowman. The different parts to the snowman were:
Math Calculations:
Area:
2 Eyes:
3 Spheres: Formula
12 inch Sphere: 904.8 In Cubed
24 inch Sphere: 7234.6 In Cubed
36 Inch Sphere: 24,416.64 In Cubed
Trigonometry
Bowtie:
h=√3/2⋅a
After substituting a=1 for 1 inch of the bowtie we have:
h=√3/2⋅1
h=√3/2
Carrot Nose:
Base: 2
Height: 5
side b: 5.0990195135928
base angle θ: 78.690
area S: 5
Reflection
We all took on different parts of the problem.
Noah:
- 3 Spheres (Volume)
- 2 Eyes (Area)
- A Bowtie (Trigonometry)
- A Top Hat (Area)
- Carrot Nose (Trigonometry)
Math Calculations:
Area:
2 Eyes:
- Area (Circle) = (3.14) r squared
- 1 inch radius
- 3.14 x 1 = 3.14 in
Top Hat: - Area (Rectangle) = L x W
- 5 x 8 = 40
- Area (Circle) = (3.14) r squared
- A (big circle) = (3.14) x 8 = 25.12
- A (little circle) = (3.14) x 5 = 15.7
- 25.12 - 15.7 = 9.42 in
3 Spheres: Formula
12 inch Sphere: 904.8 In Cubed
24 inch Sphere: 7234.6 In Cubed
36 Inch Sphere: 24,416.64 In Cubed
Trigonometry
Bowtie:
h=√3/2⋅a
After substituting a=1 for 1 inch of the bowtie we have:
h=√3/2⋅1
h=√3/2
Carrot Nose:
Base: 2
Height: 5
side b: 5.0990195135928
base angle θ: 78.690
area S: 5
Reflection
We all took on different parts of the problem.
Noah:
- Trigonometry
- Habits of a Mathematician: Collaborate and Listen
- Area
- Habits of a Mathematician: Take apart and put back together
- Volume
- Habits of a Mathematician: Conjecture and test
What would we do differently next time?
Next time I would want to do possibly a building of some sort. I think a building would be a good problem.